题目描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
解题方法
二叉树深度遍历、二叉树层序遍历(其实就是两种不同的遍历顺序而已,哪个习惯用哪个)没学过的可以去看看左神的视频
思路
题目分析
写写简单题水一水( •̀ ω •́ )y
根据题目给的示例得知:
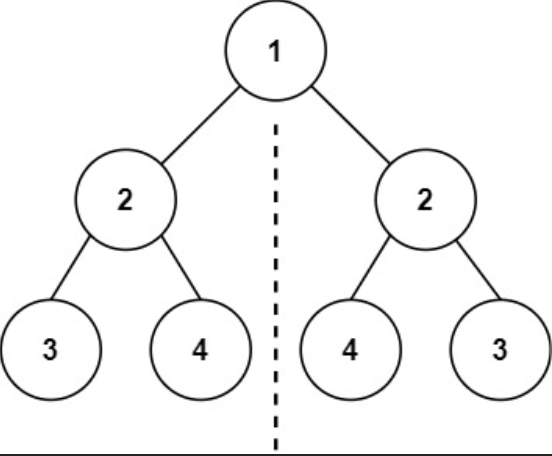
我们沿着根节点向下判断:
- root->left =? root->right
- left->left =? right->right
- left->right =? right->left
- 因为是判断对称,所以我们需要判断左子树左子树和右子树右子树以及左子树的右子树和右子树的左子树是否相等,所以我们可以将这颗二叉树“沿对称轴剪开”看成根节点相同的两颗二叉树,然后进行上面的判断,不难发现上面的定义是递归的>w<
- 当然,我们也可以逐层判断得到当前层的节点(即left->left, right->right和left->right,right->left),当前层判断完后,按顺序将下一层的节点放入,然后再按顺序弹出判断
细节
许多人可能兴致冲冲的写完,发现折在了null节点上。我们来想一想, 假设这颗二叉树左侧有一个节点为空,如果想让这颗为叉树对称,是不是需要这个空节点的对称位置也为空?通过前面的分析我们得知,我们是按照对称的位置顺序遍历的,所以我们只需要判断当前遍历到的节点是否都为空就好了。
代码实现
直接看代码实现吧
“`c++
//递归实现
class Solution {
public:
bool isSymmetric(TreeNode* root)
{
return f1(root, root);//将二叉树拆分为两部分,同时遍历
}
<pre><code>bool f1(TreeNode* left, TreeNode* right)
{
if(!left && !right) return true;//只有对称位置都为空,才能称得上对称
//只有一侧节点为空,或者值不相等都称不上对称
if((!left || ! right) || (left->val != right->val)) return false;
//继续判断 左子树的左侧 与 右子树的右侧是否相等 以及 左子树的右侧 与右子树的左侧是否相等
return f1(left->left, right->right) && f1(left->right, right->left);
}
</code></pre>
};
<pre><code class="wp-editormd-codeblock line-numbers">> 可以将f1的定义理解为,判断以当前节点为根的两个子树是否对称 或者 值是否相等。当前子树的又可以拆分为 这个节点本身 + 去除这个节点的子树
下面是层序遍历的代码,和普通的层序遍历差别不大,注意节点插入和弹出顺序就好
</code></pre>
class Solution {
public:
bool isSymmetric(TreeNode* root)
{
return f2(root, root);<br />
}
<pre><code>bool f2(TreeNode* left, TreeNode* right)
{
queue<TreeNode*> q;
q.push(left);
q.push(right);
while(!q.empty())
{
TreeNode* l = q.front(); q.pop();
TreeNode* r = q.front(); q.pop();
if(!l && !r) continue;
if((!l || ! r) || (l->val != r->val)) return false;
q.push(l->left);
q.push(r->right);
q.push(l->right);
q.push(r->left);
}
return true;
}
</code></pre>
};
“`
注意 :我们入队时先进入的时左树节点,所以出队时第一个出队的也是左树节点,先进先出,记好当前的q.front()是哪个节点


